METODOS DE ARANDELAS Y CAPAS CILINDRICAS

METODO DE ARANDELAS.

El método de Arandelas o Washer, es una extención del método de discos para sólidos huecos. Donde se tiene un radio interno r y un radio R externo de la arandela.

La integral que contiene el radio interno representa el volumen del hueco y se resta de la integral que contiene el radio externo.

El volumen viene dado por:

Ejemplo:

METODO DE CAPAS CILINDRICAS.

Nuevamente, estamos trabajando con un sólido de revolución. Como antes, definimos una región R, acotada arriba por la gráfica de una función y = f (x), abajo por el eje x y a la izquierda y derecha por las rectas x = a y x = b, respectivamente, como se muestra en la Figura 6.9 (a). Luego giramos esta región alrededor del eje y, como se muestra en la Figura 6.9 (b). Tenga en cuenta que esto es diferente de lo que hemos hecho antes. Anteriormente, las regiones definidas en términos de funciones de x giraban alrededor del eje x o una línea paralela a él.

Figura 6.9 (a) Una región delimitada por la gráfica de una función de x. (b) El sólido de revolución formado cuando la región gira alrededor del eje y.

Como lo hemos hecho muchas veces antes, “particionamos” el intervalo cerrado [a, b] usando una partición regular, P = {x0, x1, …, xn} y, para i = 1, 2, …, n, elija un punto xi* ∈ [xi − 1, xi]. Luego, construya un rectángulo sobre el intervalo [xi − 1, xi] de altura f (xi*) y ancho Δx. Un rectángulo representativo se muestra en la Figura 6.10 (a). Cuando ese rectángulo gira alrededor del eje y, en lugar de un disco o una arandela, obtenemos una cáscara cilíndrica, como se muestra en la siguiente figura.

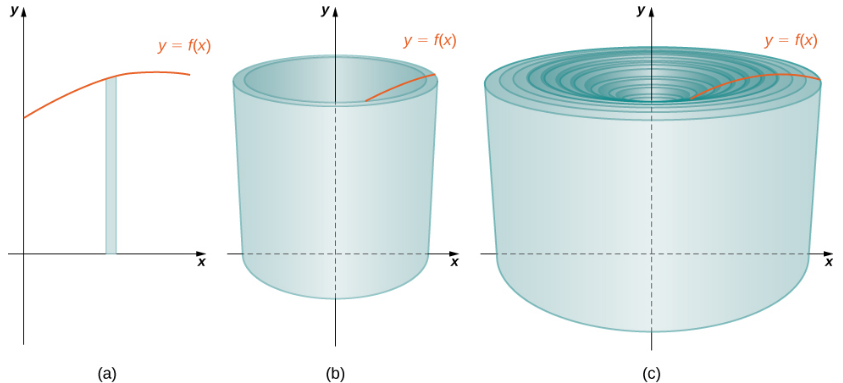
Figura 6.10 (a) Un rectángulo representativo. (b) Cuando este rectángulo gira alrededor del eje y, el resultado es una cáscara cilíndrica. (c) Cuando juntamos todas las capas, obtenemos una aproximación del sólido original.

Para calcular el volumen de este caparazón (carcasa, cáscara), considere la Figura 6.11.

Figura 6.11  Cálculo del volumen de la cáscara.

La carcasa es un cilindro, por lo que su volumen es el área de la sección transversal multiplicada por la altura del cilindro. Las secciones transversales son anillos (regiones en forma de anillo, esencialmente círculos con un orificio en el centro), con radio externo xi y radio interno xi − 1. Por lo tanto, el área de la sección transversal es

La altura del cilindro es f (xi*). Entonces el volumen V del caparazón es

Tenga en cuenta que si xi − xi − 1 = Δx, entonces tenemos

Además, (xi − xi − 1)/2 es tanto el punto medio del intervalo [xi − 1, xi] como el radio promedio del cascarón, y podemos aproximar esto por xi*. Entonces tenemos

Otra forma de pensar en esto es imaginar en hacer un corte vertical en el caparazón y luego abrirlo para formar una placa plana (Figura 6.12).

Figura 6.12 (a) Haga un corte vertical en una carcasa representativa. (b) Abra la carcasa para formar una placa plana.

En realidad, el radio exterior de la carcasa es mayor que el radio interior y, por lo tanto, el borde posterior de la placa sería ligeramente más largo que el borde frontal de la placa. Sin embargo, podemos aproximar la carcasa aplanada por una placa plana de altura f (xi*), ancho 2π xi* y espesor Δx (Figura 6.12). El volumen de la carcasa, entonces, es aproximadamente el volumen de la placa plana. Multiplicando la altura, el ancho y la profundidad de la placa, obtenemos

que es la misma fórmula que teníamos antes.

Para calcular el volumen de todo el sólido, agregamos los volúmenes de todas las capas y obtenemos

Aquí tenemos otra suma de Riemann, esta vez para la función 2πx f(x). Tomar el límite cuando n → ∞ nos da

Esto lleva a la siguiente regla para el método de las capas cilíndricas.