AREA BAJO CURVAS

La interpretación geométrica de la regla de Barrow nos dice que la integral definida representa el área entre la curva y el eje de abscisas.

Área bajo la curva

Esto es cierto si la curva es positiva en el intervalo [a,b], es decir, si está por encima del eje OX.

Si estuviese por debajo, nos saldría un resultado negativo (tomando valor absoluto se soluciona el problema).

Sin embargo, hay veces en que la curva tiene partes por debajo y partes por encima

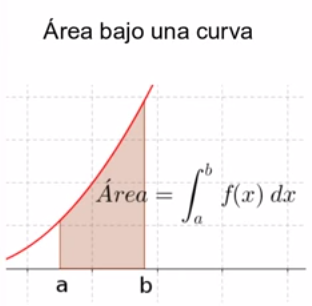
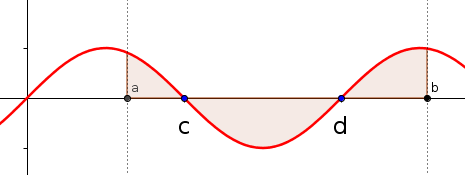
Si hacemos la integral definida entre a y b nos conduciría a un resultado erróneo. Habría que descomponer la integral en tres partes correspondientes a los intervalos [a,c] [c,d] y [d,b] y además tener en cuenta que en el intervalo [c,d] debemos tomar valor absoluto (porque saldría un área negativa al estar por debajo del eje).

Lo más práctico es tomar valor absoluto en todos los intervalos (y así no necesitamos saber los que están por encima y los que están por debajo). El área (A) de la imagen anterior se calcularía así:

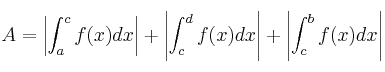
¿Cómo saber si la curva f(x) corta al eje X dentro del intervalo [a,b]?

Basta con resolver la ecuación

y ver si alguna de las soluciones está dentro del intervalo [a,b].

Si al resolver la ecuación

obtenemos que entre las soluciones hay dos (c y d) dentro del intervalo, calcularíamos el área con la fórmula:

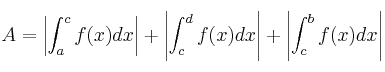
EJEMPLO:

Halla el área que delimita la gráfica de la función con el eje de abscisas entre las rectas y

SOLUCIÓN

Nos están pidiendo el área bajo una curva en el intervalo [0,2], es decir, el área limitada por la curva, el eje de abcisas y las rectas verticales x=0 y x=2.

Si miramos la teoría, debemos resolver la ecuación y ver si alguna de las soluciones está dentro del intervalo.

En nuestro caso la función es y el intervalo

Resolvemos y obtenemos como soluciones y . La solución si está dentro del intervalo , por tanto debemos considerarla y dividir el intervalo en dos: y , quedando así nuestra fórmula para calcular el área:

$A = \left|\int_0^1 (x^2-4x+3) dx \right|+ \left|\int_1^2 (x^2-4x+3) dx \right|$

Calculamos primero la integral indefinida:

$\int (x^2-4x+3) dx = \frac{x^3}{3} - \frac{4x^2}{2} + 3x = \frac{x^3}{3} - 2x^2 + 3x$

Y ahora le aplicamos los límites de integración

$\int_0^1 (x^2-4x+3) dx= \left[ \frac{x^3}{3} - 2x^2 + 3x \right]_0^1 =$

$= \left[ \frac{1^3}{3} - 2 \cdot 1^2 + 3 \cdot 1 \right] - \left[ \frac{0^3}{3} - 2 \cdot 0^2 + 3 \cdot 0 \right] = \frac{4}{3}$

$\int_1^2 (x^2-4x+3) dx= \left[ \frac{x^3}{3} - 2x^2 + 3x \right]_1^2 =$

$= \left[ \frac{2^3}{3} - 2 \cdot 2^2 + 3 \cdot 2 \right] - \left[ \frac{1^3}{3} - 2 \cdot 1^2 + 3 \cdot 1 \right] = \frac{2}{3} -\frac{4}{3} = \frac{-2}{3}$

Recordemos que tenemos que expresarlo en valor absoluto

$A = \left|\int_0^1 (x^2-4x+3) dx \right|+ \left|\int_1^2 (x^2-4x+3) dx \right| = \left| \frac{4}{3} \right| + \left| \frac{-2}{3} \right| = \frac{6}{3} = 2 \: u^2$

En la siguiente imagen podemos ver como el área representa 2 unidades cuadradas