TEOREMA DEL VALOR MEDIO PARA INTEGRALES.
Este teorema es importante porque asegura que una función continua en un intervalo cerrado alcanza su valor promedio al menos en un punto.
- Si f es continua en el intervalo cerrado [a, b], existe un número c en este intervalo tal que
f(c)(b - a) = ![]()
Demostración:
Primer caso: Si f es constante en el intervalo [a, b] el resultado es trivial puesto que c puede ser cualquier punto.
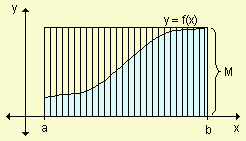
Segundo caso: Si f no es constante en [a, b] elegimos m y M como el menor y mayor valor que toma f en el intervalo. Dado que m £ f(x) £ M " x Î [a, b] por el teorema de conservación de desigualdades.Aplicando propiedades:
m(b - a) ![]() M(b - a) entonces m
M(b - a) entonces m ![]() M.
M.
Dado que f es continua el teorema del valor intermedio asegura que f alcanza cada valor entre su mínimo y su máximo. Por lo tanto permite deducir que debe alcanzar el valor ![]() en algún punto c del intervalo. [a, b]. Queda demostrado que existe algún c tal que f(c) =
en algún punto c del intervalo. [a, b]. Queda demostrado que existe algún c tal que f(c) = ![]() .
.
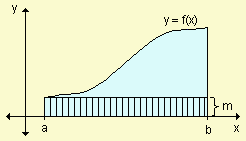
Interpretación gráfica del teorema para una función positiva:
|
|
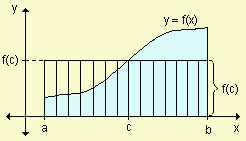
rectángulo inscripto (área menor que la de la región)
| rectángulo del valor medio (área igual que la de la región)
|
| rectángulo circunscripto (área mayor que la de la región)
|
El valor de c no es necesariamente único. Este teorema no especifica cómo determinar c. Solamente garantiza la existencia de algún número c en el intervalo. Permite una interpretación interesante para el caso en que f es no negativa en [a, b]. En este caso ![]() es el área bajo la gráfica de f entre a y b. El teorema asegura que existe un valor c del intervalo al que está asociado f(c) que corresponde a la altura del rectángulo de longitud de la base (b - a) y su área coincide con la de la región.
es el área bajo la gráfica de f entre a y b. El teorema asegura que existe un valor c del intervalo al que está asociado f(c) que corresponde a la altura del rectángulo de longitud de la base (b - a) y su área coincide con la de la región.
| A = | 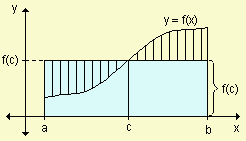 |
El valor de f(c) hallado según el teorema del valor medio para integrales coincide con el valor promedio o medio de una función por eso a f(c) = ![]() se lo llama valor medio de f en el intervalo [a, b].
se lo llama valor medio de f en el intervalo [a, b].
Ejemplo: halle el valor promedio de f(x) = 3x2 - 2x en el intervalo [1, 4].
Calculamos:
fprom = ![]() =
= ![]() =
= 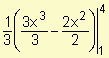 =
= ![]() (64 - 16 -1 + 1) = 16
(64 - 16 -1 + 1) = 16
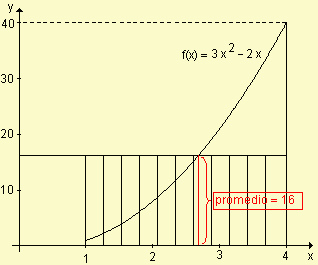
Sabemos que el área de la región es igual al área del rectángulo cuya altura es el valor promedio. Se puede observar gráficamente.